Regularity and Connectedness of Pareto-Optimal Solutions

Regularity and connectedness are general properties of multi-objective optimization problems that is not problem-specific. These properties include
• Pareto-optimal solutions are often connected, or piecewisely connected.
• The distribution of Pareto-optimal solutions, i.e., the Pareto-front or Pareto surface, are often of low order
• According to the Karush-Kuhn-Tucker conditions, for continuous multi-objective problems with m objectives, the Pareto-front is a (m-1)-dimensional piecewise continuous manifold

Researchers in the evolutionary optimization community have not paid sufficient attention to take advantage of resularity and connectedness of Pareto-optimal solutions to improve the performance of multi-objective evolutionary algorithms, although the success of combining local search in evolutionary algorithms can mainly attributed to these properties [1]. In the recent years, we have performed research on developing evolutionary algorithm that are able to take advantage of connectedness and regularity properties. These algorithms include the dynamic weighted aggregation method [2-4], and the modeling regularity in evolutionary multi-objective optimization using edtimation of distribution algorithms [5-7]. The main differences between single-objective optimization and multi-objective optimization, which are most essential in developing efficient and scalable evolutionary multi-objective optimization algorithms, have been elaborated in [8].

Dynamic Weighted Aggregation for Evolutionary Multiobjective Optimization

Conventional weighted aggregation (CWA) is an intuitive way for multiobjective optimization. In this approach, different objectives are weighted and summed up to one single objective. Take a bi-objective problem as an example:

F = w₁f₁ +w₂f₂,
where w₁ and w₂ are non-negative weights with w₁ + w₂ = 1, f₁ and f₂ are two conflicting objectives. Conventionally, the weights are fixed during optimization. The following conclusions can be drawn for the conventional weighted aggregation (CWA):

• It is computationally very efficient
• It is conceptually very easy to understand
• Only one solution can be obtained in one run, assuming that the Pareto front is convex
• The solutions located in the concave region of the Pareto front cannot be obtained.
An evolutionary dynamic weighted aggregation has been proposed in [2,3,4]. This method proposes a brand-new concept on multiobjective optimization using weighted aggregation. The key aspects of the concept are:

• For a convex Pareto front, each weight combination corresponds to a stable minimum on the Pareto front.
• For a concave Pareto front, all solutions with exception to the two points on the two ends are unstable minima. Therefore, an optimization algorithm will converge to either of the two points whatever weight combination is used.
• When the Pareto front is rotated slowly, meaning the weight combination is changed gradually during optimization, the optimizer will move from one stable minimum to another, once it has reached any point of the Pareto front. If the pareto front is convex, the moving speed is determined by the change of the weights. If the Pareto front is concave, the optimizer will stay on one stable minimum until the minimum becomes unstable. In this case, the optimizer will be able to move along the Pareto front to the next stable minimum.
Refere to Figures 1 and 2 for an illustration. Fig. 1. A convex Pareto front. Each point on the Perato front is a stable minimum corresponding to a given weight combination (a rotation angle). Fig. 2. A concave Pareto front. Only the two points at the two ends of the Pareto front are stable minima.

According to this theory, the whole Pareto set can be obtained by

• changing the weight (say w1) gradually from 0 to 1 (or 1 to 0) generation by generation during optimization.
• switching the weight (say w1) between 0 and 1. Notice that the switching should be done after the optimizer has conveged to one stable minimum on the Pareto front and the switching period should be larger that one generation.

Preliminary result from an example with 3 objectives is shown in Fig. 3. The weights are changed as following:

w₁ = sin(2 &trade t/F);
w₂ = (1-w₁)*sin(2&Pi t/F);
w₃ = (1-w₁ -w₂).

The projections onto three two-dimensional spaces, i.e., (f₁, f₂), (f₂, f₃), (f₃, f₁) are in Fig. 4. A 3D picture of the analytical Pareto-optimal surface is shown in Fig.5. (Thanks to Oliver Schütze, Dept. of Mathematics and Computer Science, University of Paderborn for proving me this picture.)

Fig. 3. Pareto-optimal solutions for a 3-objective test function.
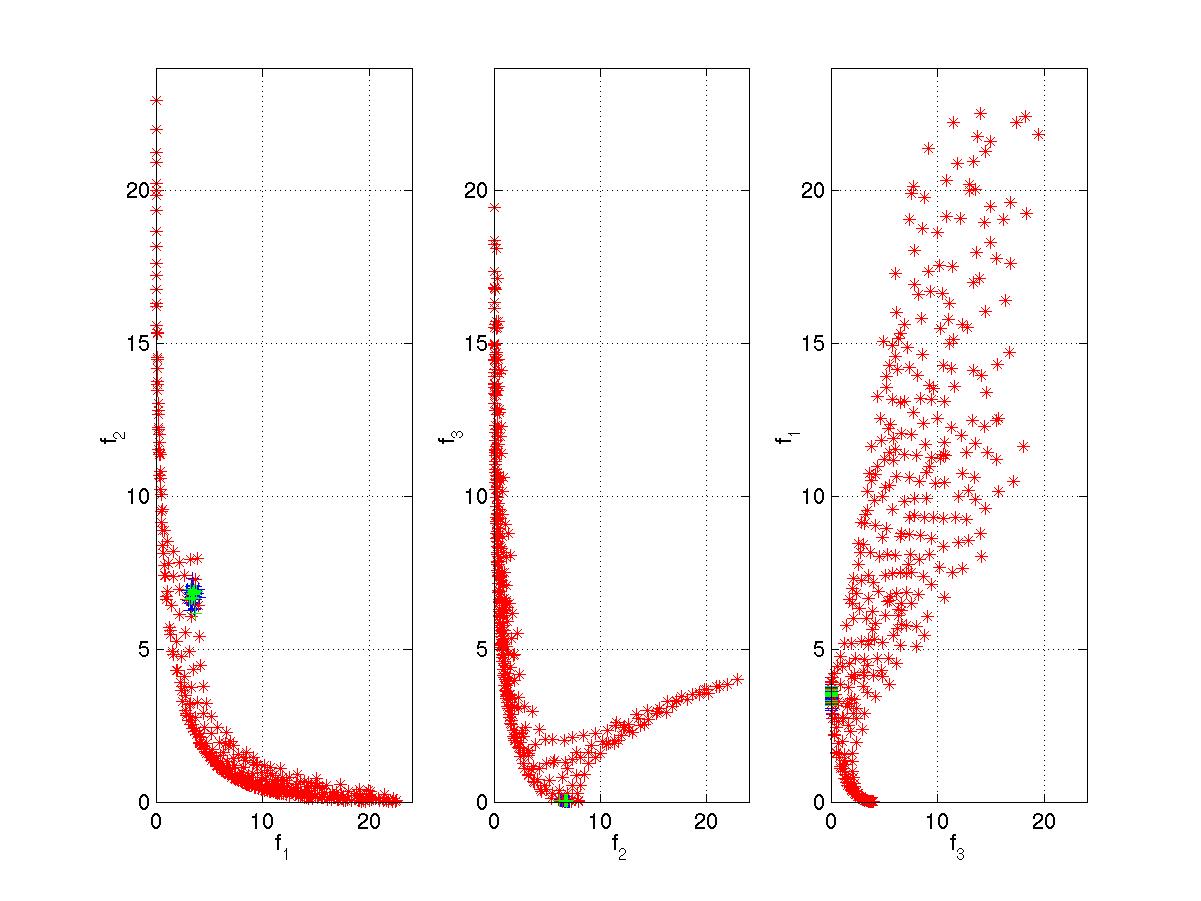
Fig. 4. The projections of the obtained Pareto-optimal surface.


Fig. 5. The analytical Pareto-optimal surface.
It has been shown on several test functions that the evolutionary dynamic weighted aggregation methods work very efficiently, no matter whether the Pareto front is convex or concave. In general, the following conclusions can be reached for the EDWA:

• It is computationally very efficient and conceptually very easy.
• It is able to obtain the whole Pareto set in one run.
• It is able to handle both convex and concave Pareto fronts.

From the above conclusions, it can be seen that the EDWA has overcome the two main weaknesses of the weighted aggregation based approach to multiobjective optimization.

Readers are referred to the references [2-4] for more details.

Modeling Regularity explicitly in Multi-Objective Optimization (Mr-MOO)

Refer to [5-7] for details.

References

[1] Y. Jin and B. Sendhoff. Connectedness, regularity and the success of local search in evolutionary multi-objective optimization. In: Proceedings of the IEEE Congress on Evolutionary Computation, Vol.3, pp.1910-1917, 2003
[2] Y. Jin, T. Okabe and B. Sendhoff. Adapting weighted aggregation for multiobjective evolution strategies. First International Conference on Evolutionary Multi-criteria Optimization, LNCS 1993, pp.96-110, Springer, 2001
[3] Y. Jin, M. Olhofer and B. Sendhoff. Dynamic weighted aggregation for evolutionary multiobjective optimization: Why does it work and how? In Genetic and Evolutionary Computation Conference, San Francisco, July 2001
[4] Y. Jin. Effectiveness of weighted sum of the objectives for evolutionary multi-objective optimization: Methods, analysis and applications. Unpublished manuscript. 2002
[5] Y. Jin, A. Zhou, Q. Zhang, B. Sendhoff, and E. Tsang. Modeling regularity to improve scalability of model-based multi-objective optimization algorithms. In: J. Knowles, D. Corne, K. Deb (eds.), Multi-Objective Problem Solving from Nature, pp. 331-356, Springer, 2008
[6] Q. Zhang, A. Zhou, Y. Jin. RM-MEDA: A regularity model based multi-objective estimation of distribution algorithm. IEEE Transactions on Evolutionary Computation, 12(1):41--63, 2008
[7] A. Zhou, Q. Zhang, Y. Jin. Approximating the set of Pareto-optimal solutions in both decision and objective spaces by an estimation of distribution algorithm. IEEE Transactions on Evolutionary Computation, 13(5):1167-1189, 2009
[8] Y. Jin and B. Sendhoff. A systems approach to evolutionary multi-objective structural optimization and beyond. IEEE Computational Intelligence Magazine, 4(3):62-76, 2009

For discussions, please contact Yaochu Jin.